Not: “Elastisite Modülü(Young Modülü) ve Hooke Kanunu“, “Poisson Oranı“, “Kesme Kuvveti – Kayma Gerilmesi” ve “Kayma Modülü(Rijitlik Modülü)” yazılarımız bir bütün olduğundan verilen sıralamayla okunmasını özellikle tavsiye ediyoruz.

Öncelikle bu yazımız okumadan önce “Elastisite Modülü(Young Modülü) ve Hooke Kanunu” isimli yazımızı da okumanızı tavsiye ederiz.

Poisson Oranı; bir malzemenin elastik bölgede yanal ve eksenel elastik birim şekil değişimlerinin oranı ile elde edilen bir sabittir. Elastisite Modülü ile ilgili olan yazımızı okursanız “Birim Şekil Değiştirme” vb. gibi terimlerin ne anlama geldiğini ve nasıl bulunduğunu daha iyi anlayacaksınızdır.

Elastisite modülünü anlatırken, tek eksenli oluşan gerilim ve deformasyonlardan bahsetmiştik. Ancak, bir malzeme, örnek olarak çekme kuvvetine maruz kaldığında, kuvvet ekseninde uzamaya maruz kalırken, diğer eksenlerde ise daralma meydana gelir. Veyahut bir malzeme basınç kuvvetine maruz kaldığında, kuvvet ekseninde kısalmaya maruz kalırken, diğer eksenlerde genişleme meydana gelir. (Daralma ve genişleme terimlerinden kasıt, enine yani yanal deformasyonlardır.) (diğer eksenler = kuvvet uygulanan eksene dik eksenler) İşte bu yanal eksenlerde oluşan birim şekil değiştirmenin, kuvvet ekseninde oluşan birim şekil değiştirmeye oranının “-“(eksi) ile çarpımı “poisson oranı“nı verir. (υ = – εy/εx)

Poisson oranı genelde “υ” veya “μ” simgeleri ile gösterilir.

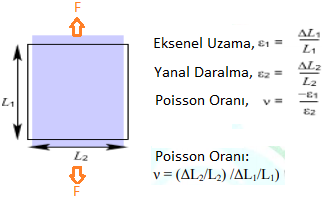
Eksenel Yönde Çekme Kuvvetine Maruz Kalan Bir Malzemenin Poisson Oranı Bağıntısı

Örneğin; poisson oranı (υ) 0,25 olan bir malzeme, gerilme kuvvetine maruz kalıyorsa ve eksenel yönde(εeksenel) 1cm. uzuyorsa, bu malzemenin yanal şekil değişimi (εyatay) (daralma) 0,25 cm. olur. (Eksenel şekil değişimi = kuvvetin uygulandığı eksende oluşan şekil değişimi, Yanal şekil değişimi = Kuvvetin uygulandığı eksene dik eksende oluşan şekil değişimi)

Tek eksenli çekme veya basınç kuvveti uygulandığında enine yani yanal şekil değişimine uğramayan bir malzeme için poisson değeri 0 olacaktır. (“υ=0”)

Uygulanan kuvvet altında kuvvet ekseni yönünde şekil değişimi oluyor ancak malzemenin hacmi değişmiyorsa teorik olarak poisson oranı 0,5 olacaktır. (“υ=0,5”) 

Malzemelerin poisson oranı 0 ile 0,5 aralığında kabul edilir. (0<υ<0,5)  Ancak auxetic malzeme olarak adlandırılan bazı malzemelerin poisson oranı negatiftir. Bu da şu anlama geliyor: Örneğin, bir malzemeye çekme kuvveti uygulanıyor. Bu kuvvet etkisiyle, kuvvet ekseninde uzama meydana geliyor. Normalde, bahsettiğimiz gibi yanal eksenlerde daralma meydana gelmesini bekleriz ancak bu malzemelerde tam tersi genişleme meydana geliyor. İşte auxetic malzeme olarak adlandırılan bu tür malzemelerin poisson oranı negatiftir ve teorik olarak en düşük “-1” değerini alırlar. Yani çoğu malzemenin poisson katsayısı 0 ile 0,5 arasında yer alsa da auxetic malzemeleri de düşününce  poisson aralığı olarak -1<υ<0,5 de diyebiliriz.

Poisson oranı, zemin malzemelerinde malzemenin suya doygunluğunu anlatan bir sabittir. Poisson sabiti 0,5 e yakın malzemelerin suya doygunluğu yüksektir ve sıkıştırılabilirliği yok denecek kadar azdır.

Sıvıların poisson oranı teorik olarak tam olarak 0,5’tir. Çünkü sıvılar sıkıştırılamazlar. Bu nedenle hiçbir katı malzemenin poisson oranı 0,5 olamaz. Yani poisson oranı 0,5 olan bir malzeme olsa idi sıkıştırılamaz ve bu nedenle de bu kuvvet altında hacim değişikliğine uğramazlar idi. Mesela; lastik, kauçuk gibi bazı malzemelerin poisson oranları 0,5 değerine yakındır.

Poisson oranı 0,5 değerine yaklaşan bir malzemenin sıkıştırılabilirliği ne kadar düşük ise, şekil değiştirmesi o kadar yüksek yani kolaydır. Bu durumda poisson oranı -1’e yaklaşan bir malzemenin ise sıkıştıralabilirliği o kadar fazla ve şekil değiştirmesi ise o kadar zordur yani şekil değişimine karşı dirençlidir. Bu durumda poisson oranı elastik malzemelerin kuvvet altında uğrayacağı deformasyonlar hakkında bilgi veren önemli bir sabittir.

Daha iyi anlaşılması için; kuvvet altındaki bir malzemenin hacmi değişmiyorsa, neden 0,5 poisson oranına sahip olması gerektiğini abartılı değerler ile bir örnek vererek anlatacak olursak;

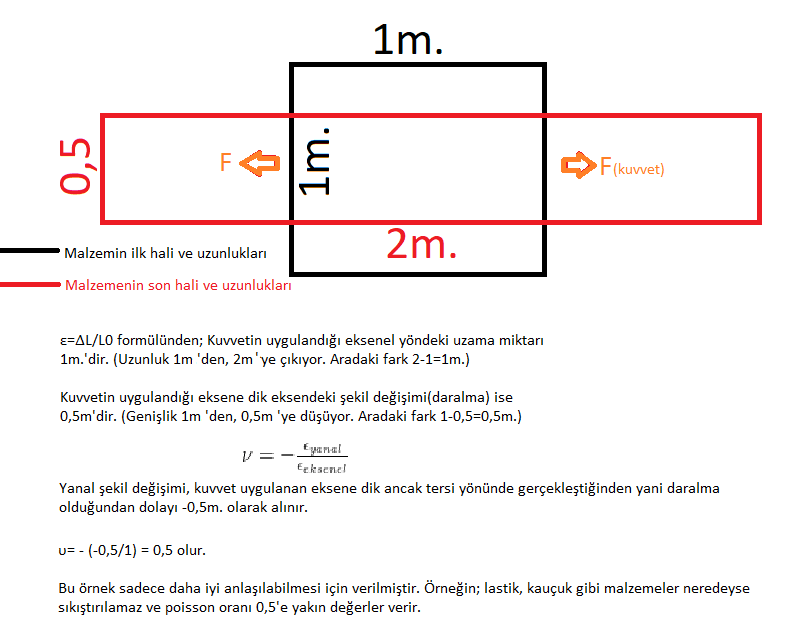
Şimdi bir malzemeyi 3 boyutlu olarak düşünürsek; 3 eksendeki poisson oranı ve bağıntılarını ve elastisite modülü bağıntılarını inceleyebiliriz.

Yukarıdaki resim ve bağlantıları incelersek; Poisson oranı ile ilgili yaptığımız açıklama ve bağıntıların aynısını üstteki turuncu alanda görüyoruz. Burada kafanız karışmasın. Burada malzemeye “Y” ekseninde(Y-düzlemi: etkime düzlemi) bir kuvvet uygulandığını görüyoruz. Bu durumda poisson değerimiz kuvvet eksenine dik olan eksenlerde oluşan birim şekil değişimlerinin, kuvvet ekseninde oluşan birim şekil değişimine oranının “-” (eksi) ile çarpılmış halidir. Kuvvet ekseni “Y” olduğuna göre; υ = – εyatay / εeksenel yani υ = – εx / εy =- εz / εy olur. Yani “y” ekseninde meydana gelen birim şekil değiştirme ile poisson oranını “Y” eksenine dik olan “X” ve “Z” eksenlerindeki şekil değişimlerini buluruz.  Elastisite modülünü anlatırken σ= E x ε bağıntısını vermiştik. Sonuç olarak bağıntıları kullanarak yeni bağıntıların elde edilmesinden başka bir şey yapmıyoruz. Dikkatli şekilde incelendiğinde çok basit olduğunu göreceksinizdir.

Not: Plastik bölgede uygulanan kuvvetlerden dolayı meydana gelen şekil değişimlerinde hacim her zaman korunur ve bu nedenle bu bölgede poisson oranından bahsetmek gerekirse poisson oranı her zaman 0,5’tir. Ancak poisson oranı belirlenirken elastik bölge ve bu bölge içerisinde gerçekleşen olaylar dikkate alınır. Elastisite modülü ve poisson oranı malzemenin kuvvet altında elastik deformasyonları sonucu hesaplanan değerlerdir.

Zemin ve kayaç türlerinde poisson oranı önemli bir değerdir. Kayaçların poisson oranı 0 ile 0,5 aralığındadır ve poisson oranı 0,5’e yaklaştıkça suya doygunlukları artar.

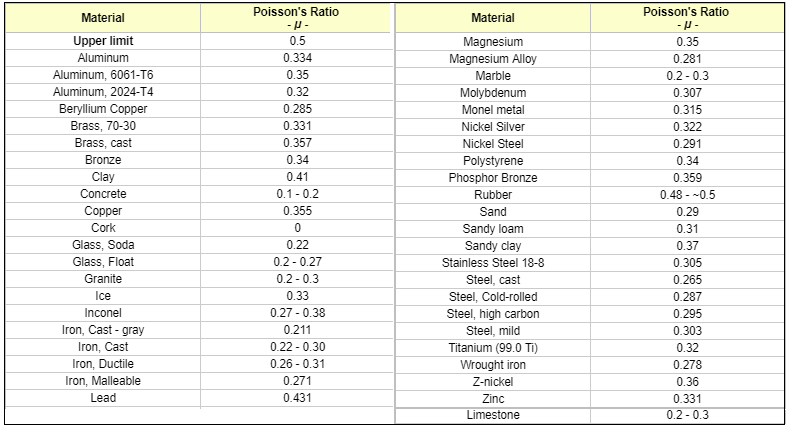
Çeşitli Malzemelerinin Çeşitli Deneyler Sonucu Yaklaşık Olarak Kabul Edilmiş Poisson Oranları

Bazı İnşaat Malzemelerinin Çeşitli Deneyler Sonucu Yaklaşık Olarak Kabul Edilmiş Poisson Oranları

Konu ile ilgili “Elastisite Modülü(Young Modülü) ve Hooke Kanunu” yazımızda belirttiğimiz kaynakları da inceleyebilirsiniz. (Bir çoğu poisson oranından da bahsetmektedir.)

Konu ile ilgili bazı kaynaklar:

Sayın Mümtaz Erdem’in hazırlamış olduğu incelenmesinde fayda gördüğümüz “Malzeme Özellikleri” isimli bir kaynak.

Sayın Muhammet Uzun’un hazırlamış olduğu “NEGATİF POİSSON ORANINA SAHİP (AUXETIC)MALZEMELER VE UYGULAMAALANLARI – NEGATIVE POISSON RATIO (AUXETIC)MATERIALS AND THEIR APPLICATIONS) isimli özellikle negatif poisson oranına sahip malzemeler ile ilgili daha geniş bilgi almak isteyenler için oldukça faydalı bir kaynak.

Bartın Üniversitesi dokümanlarından elde ettiğimiz “Malzemelerin Mekanik Özellikleri” isimli elastisite modülü, poisson oranı, kayma modülü vb. birçok konunun yer aldığı ve bunları sayısal örneklerle destekleyen güzel bir kaynak.

İ. Akkaya, A. Özvan,, M. Tapan, M. Bor ve E. Erdeve Özvan tarafından hazırlanmış “Farklı Kayalarda Ultrasonik Yöntem ile Belirlenen Poisson Oranının Kimyasal, Fiziksel ve Mekanik Özelliklerle İlişkisinin Belirlenmesi” isimli isminden anlaşılacağı üzere oldukça faydalı ve çeşitli kayaç türlerinin poisson oranlarının yer aldığı bir kaynak.

“Gerilme-Şekil Değiştirme ve Bünye Bağıntıları (Hooke Yasaları)” isimli içerisinde sayısal problemler ve çözümler bulunan oldukça faydalı bir kaynak.

“Elastik Sabitler” isimli içerisinde elastisite modülü, poisson oranı, kayma modülü ve hacimsel modül konularının yer aldığı ve bu konuların sayısal örneklerle desteklendiği incelenmesi gereken oldukça faydalı bir kaynak.

“Elastik Davranış” isimli incelenmesi gereken oldukça faydalı bir kaynak.

Not: Elastisite Modülü, Poisson Oranı, Kayma Modülü ve Hacimsel Modül elastik bölgede gerçekleşen birbirleriyle bağlantılı sabitler olmasından dolayı bu konularla ilgili yazılarımızı sırasıyla okumanızı ve sonrasında kaynaklarda yer alan sayısal örnekleri incelemenizi tavsiye ederiz. Bu şekilde bu konulara bir inşaat mühendisi olarak fazlasıyla hakim olacağınızı düşünüyoruz.